What Tool Do I Use To Find The Center Of A Circle?

A circle is a shape where all points are equidistant from a fixed point called the center. Finding the center of a circle is an important concept in geometry with many real-world applications. For example, finding the center is critical in calculating properties like circumference and area. There are various techniques to determine the center of a circle depending on the information available.

Compass Method

The compass method is one of the most common and straightforward ways to find the center of a circle. This method only requires a compass, straightedge or ruler, and a pencil. Here are the steps to use a compass to determine the center of a circle:

1. Draw any straight line between two points on the circumference of the circle. This line is called a chord.
2. Place the point of the compass on one end of the chord, and open it to be longer than the chord length. Draw an arc above the chord extending just past the edge of the circle on both sides.
3. Leave the compass at the same width. Place the point on the other end of the chord, and draw another arc under the chord extending past the edge of the circle on both sides.
4. The two arcs will intersect at two points. Draw a straight line connecting the points of intersection. This line will go through the center of the circle.

The compass method utilizes basic geometry about chords, radii, and arcs to determine the midpoint of a circle accurately. By creating two congruent arcs from points along a chord, the intersection of these arcs will always bisect the chord and go through the center point. This straightforward compass technique has been used for centuries and continues to be a popular way to find circle centers for drawing, construction, design, and more.

For complete instructions and illustrations of using a compass to determine circle centers, refer to the wikiHow article 4 Ways to Find the Center of a Circle.

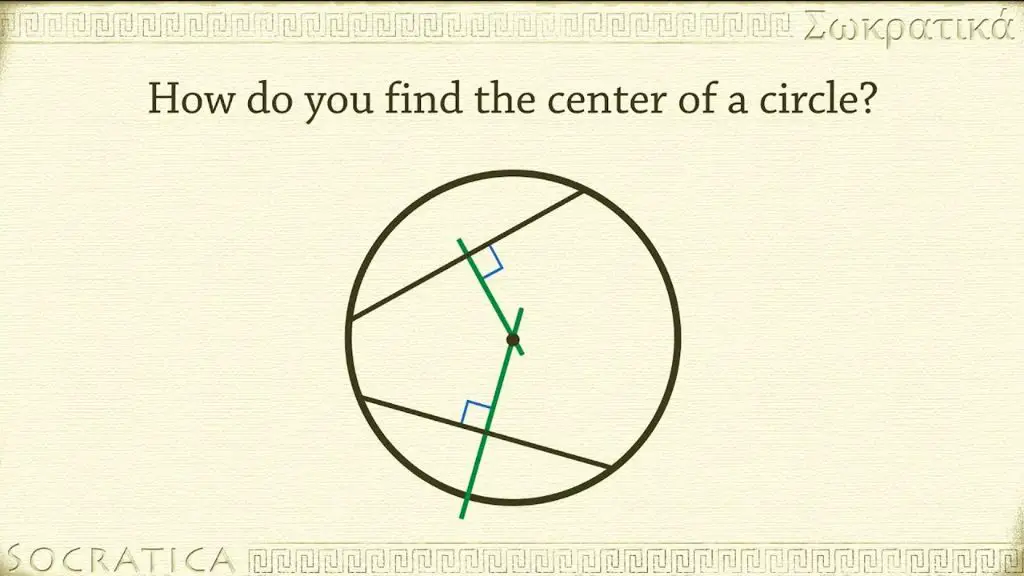
Perpendicular Bisector Method

One method to find the center of a circle is by using perpendicular bisectors. According to the theorem that the perpendicular bisector of a chord passes through the center of a circle, we can use perpendicular bisectors of two chords to locate the center.

To use this method:

1. Draw any chord across the circle.
2. Construct the perpendicular bisector of that chord using a ruler and compass. This perpendicular bisector will pass through the center of the circle.
3. Repeat steps 1 and 2 with a different chord on the circle. The intersection point of the two perpendicular bisectors is the center of the circle.

The reason this method works is that the perpendicular bisector of a chord will always bisect it into two equal halves and pass through the center point. By constructing perpendicular bisectors of two different chords, the intersection point is equidistant from the endpoints of both chords, meaning it must be the center of the circle.

This is an easy way to find the center of any circle using basic geometry concepts. With just two perpendicular bisectors, the center can be accurately located.

Paper Folding Method

The paper folding technique is a simple way to find the center of a circle using just a piece of paper. Here are the steps:

1. Draw a circle on a rectangular piece of paper. Make sure the circle is contained within the paper and doesn’t touch the edges.
2. Fold the paper in half horizontally, creasing along the fold.
3. Now fold the paper in half vertically, creasing along the new fold.
4. Unfold the paper. The two crease lines will intersect at the center of the circle.
5. You can mark the center point or put a pushpin through it to clearly identify the center of the circle.

This technique works because when you fold the paper both horizontally and vertically, the folds will always meet at the midpoint of the paper. With the circle drawn anywhere on the paper, the midpoint of the paper aligns with the center of the circle. The crease lines created by the folds will intersect right at the circle’s center point.

For a step-by-step visual guide of this method, refer to this source: Circle Center by Paperfolding

Coordinate Method

The coordinate method is a straightforward way to find the center of a circle using the coordinates of points that lie on the circle. This method relies on the equation of a circle:

(x – h)2 + (y – k)2 = r2

Where (h, k) are the coordinates of the center and r is the radius.

To find the center using coordinates:

1. Pick any two points on the circle and record their coordinates (x1, y1) and (x2, y2).
2. Plug these coordinates into the circle equation and create two equations.
3. Set the equations equal and solve the system of equations to find h and k.

For example, say we have points A(-2, 5) and B(4, 3) on a circle. Plugging these into the circle equation gives:

(x + 2)2 + (y – 5)2 = r2

(x – 4)2 + (y – 3)2 = r2

Setting them equal and solving gives the center point (1, 4).

Using coordinates of points on a circle in this way provides a straightforward method to calculate the center. Just plug points into the equation and solve![Source]

Median Intersecting Chords Method

The median intersecting chords method is a simple way to find the center of a circle using basic geometry. Here are the steps:

1. Draw any chord across the circle. This chord will be called chord AB.
2. Draw another chord that crosses chord AB at right angles. This chord will be called chord CD.
3. The two chords will intersect at their midpoint. Draw a line connecting the midpoints of the two chords.
4. The center of the circle lies along the line connecting the midpoints.
5. To find the precise center, simply draw the perpendicular bisector of the line connecting the midpoints. The intersection of the perpendicular bisector and the line between midpoints is the center.

This method allows you to find the center of any circle as long as you can draw two intersecting chords on it. The key is using the fact that chords intersect at their midpoints to locate the center along that intersection line. It’s a straightforward way to find the center without needing to know the radius or diameter. With just a compass and straightedge, you can mark and connect chord midpoints to determine the circle’s center.

For a visual demonstration, check out this video on finding the center using chords: How to find the centre of a given circle

Angle Bisector Method

The angle bisector method is a simple way to find the center of a circle using basic geometry. Here are the steps:

1. Draw any chord across the circle. This segment connects two points on the circle.
2. Construct the perpendicular bisector of the chord. The perpendicular bisector intersects the chord at its midpoint.
3. Draw two other chords that intersect the first chord at its midpoint. These lines trisect the original chord.
4. Construct the angle bisectors of the two angles created by the trisected chords. The angle bisectors intersect at the center of the circle.

To explain further, when two chords intersect at the midpoint of the first chord, they create two isosceles triangles. The angle bisector of an isosceles triangle goes through its vertex point and bisects its base. Since the base of each isosceles triangle is the same (the midpoint of the original chord), the angle bisectors intersect at the center of the circle.

This method relies on simple geometric concepts to find the center in a few steps. All that is needed is a compass and straightedge. The angle bisector method provides an efficient way to determine the center of any circle using basic construction techniques.

Optical Method

The optical method is a simple way to find the center of a circle using basic principles of optics and geometry. This method relies on creating identical right triangles that allow you to pinpoint the center visually.

To use the optical method, start by placing the circular object on a flat surface. Darken the edges of the circle if needed to make them more visible. Then take two thin, straight objects such as pencils or rulers and place one at the top of the circle and the other on the right side, so they intersect at the circle. Adjust them so they just touch the edge of the circle and form 90 degree angles.

Next, move your head down so your eye is along the horizontal object. Line up the vertical and horizontal objects so they appear as a plus sign (+). Then close one eye and move your head slowly up and down. When the + stays centered in your vision, mark this spot. This is where the two objects intersect at the center of the circle.

The key is that the vertical and horizontal objects will form identical right triangles with the radius as the hypotenuse. So when the legs of the triangles line up in your vision, you have found the center point. With some practice, this simple optical method allows you to accurately locate the center of any circular object.

Computer Software

Computer software can be a quick and convenient way to determine the center of a circle if the necessary information is already available. Many math and geometry programs have built-in tools to calculate circle centers and radii. Here are some common options:

Spreadsheet software like Microsoft Excel and Google Sheets have formulas that can find a circle’s center point if you input the endpoints of a diameter or the coordinates of three points on the circle’s edge. The formulas are based on the midpoint formula for diameters or solving three simultaneous equations for three points. For example, in Excel you could use the formulas =AVERAGE(A1,B1) and =GEOMEAN(A1,A2,A3) respectively.

Mathematical and CAD software often include circle calculation features as well. Programs like Mathematica, Maple, Mathcad, AutoCAD, Solidworks, etc. allow entering circle equations and geometries to output the center point and radius. The calculations are done automatically based on the input data.

There are also many free online circle calculators that can find circle centers. Websites like Symbolab and CalculatorSoup accept coordinates, radii, or equations and return the full parameters. These tools provide a quick way to check work or perform basic circle calculations.

Overall, utilizing existing software can save time determining circle centers compared to manual methods. With the right inputs, these programs automate the calculations by applying the necessary geometric formulas and algorithms.

Conclusion

There are a number of methods that can be used to find the center of a circle. The most common and simplest methods involve using basic geometry tools like a compass, straightedge, angle bisector or paper folding techniques. More advanced methods utilize concepts like coordinate geometry, chords and medians to mathematically determine the circle’s center. There are also optical techniques involving mirrors or computer software that can accurately calculate a circle’s center.

In summary, the center of a circle is an important concept in geometry and there are a variety of straightforward techniques available to identify it. The choice of method will depend on the tools available, the required accuracy and whether the circle center needs to be physically marked or just mathematically determined. With practice, most of these techniques can be readily mastered. Knowing how to find a circle’s center is a useful skill with many practical applications in fields like engineering, construction and design.